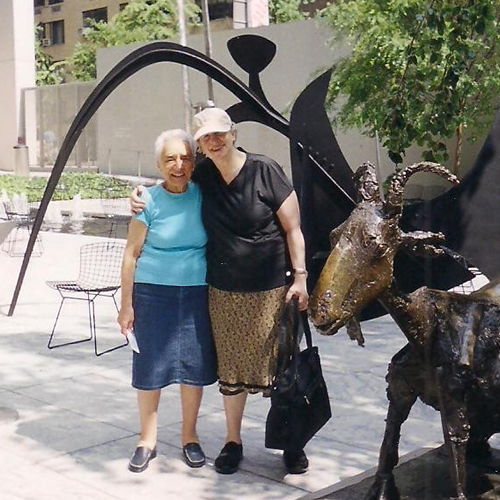- Álbum da Ciencia
- Documentación
- Ligazóns
- Videos
- Audios
- Créditos
- Agradecementos
- Bibliografía
- Publicacións CCG
María Josefa Wonenburger
Oleiros (A Coruña), 1927 - A Coruña, 2014Os ollos de María Wonenburger deixan ver a luz e a forza que sempre acompañaron esta muller. Unha persoa ben particular, que viviu coa paixón que provoca o mundo das matemáticas en sensibilidades como a dela.
O seu percorrido vital demostra unha gran valía persoal e científica. Singular estudante, lonxe da súa familia e da súa terra. Primeira bolseira Fullbright de Matemáticas en España. Doutora en Yale. O seu esforzo por chegar a ser unha investigadora e docente universitaria, sempre consciente dos obstáculos para o poder conseguir no seu país, foi axiña recompensado: no Canadá foi a única muller docente e nos EE UU gañou nos anos 70 do século XX o posto de Full Professor (equivalente a catedrática).
Ao ser unha muller nacida no ano 1927, pasou extraordinarias dificultades para atinxir as súas metas, que non eran máis que traballar e vivir do que máis lle gustaba: ensinar e investigar as matemáticas. A súa partida cara a Madrid na posguerra, a viaxe en barco aos Estados Unidos, os atrancos que atopou para se establecer alá, o seu periplo por varias universidades americanas ata a súa renuncia final por motivos persoais: todo en conxunto móstranos a coraxe dunha persoa á que lle tocou vivir tempos escuros para a ciencia en España, tempos difíciles para as mulleres que querían escapar do destino imposto. Triunfou pola súa intelixencia e pola súa constancia, mais quedoulle o resaibo amargo de non poder traballar no seu país.
Wonenburger é unha destacada alxebrista, coñecida por marcar os primeiros pasos da chamada teoría de Kac-Moody, que co andar dos anos chegaría a desempeñar un papel importante nas matemáticas e na física. Ten un brillante currículo investigador e docente, reflectido nunha chea de publicacións. Unha vida profesional moderna como a que agora desexa levar a cabo a mocidade investigadora, mais inusual na súa época.
Na ciencia e na cultura son tan importantes as conquistas alcanzadas como as persoas que as conseguen. Por iso o saber e a traxectoria de María Wonenburger espertan a simpatía polas matemáticas, mesmo en quen as considera disciplina complicada. A vida académica e científica de María rompeu con todos os modelos; o seu proceder, nada habitual, aínda hoxe sería vangardista e arriscado; a inquedanza, a constancia e a decisión son un reflexo da súa calidade persoal. Quen coñece esta muller culta, incansable lectora, de ollar amigable, melómana, deportista e amante do mar, admira a súa vontade de ser feliz e o enriquecedora que resulta a súa compañía. Unha gran muller nun corpo miúdo.
Resulta inexplicable que se puidese estar tan preto dela sen o saber. O pobo galego e a comunidade científica española coñeceron a María Wonenburger hai aínda pouco tempo, logo da publicación da súa biografía no ano 2006. Porén a magnitude do tesouro achado é tal que levou ás sociedades científicas e ás institucións, primeiro, a abraiarse de ter cerca unha figura mundial das matemáticas; despois, a outorgarlle un recoñecemento máis que merecido.
Como citar: María Josefa Wonenburger. Publicado o no Álbum de Galicia (Consello da Cultura Galega) https://consellodacultura.gal/album-de-galicia/detalle.php?persoa=4247. Recuperado o 18/04/2024
María Josefa Wonenburger
Oleiros (A Coruña), 1927 - A Coruña, 2014Autoría: Ana Dorotea Tarrío Tobar
Autoría: María José Souto Salorio
Matemática que creou unha escola internacional de Álxebra
Formación e percorrido profesional
María Wonenburger naceu en Oleiros, poboación próxima á cidade de Coruña na que a súa familia pasaba as temporadas estivais. Realizou os seus estudos de primaria e secundaria na devandita cidade, finalizando estes últimos no ano 1944 no instituto Eusebio da Guarda. Eran tempos difíciles, tanto o período da guerra civil como os anos posteriores.
Desde pequena María coñecía o gusto dos seus pais: que estudase unha enxeñería para perpetuar o negocio do seu pai, Xullo Wonenburger, quen rexentaba unha coñecida fundición na Coruña. Sen embargo, ela desde sempre quixo dedicarse ás Matemáticas e a súa familia respectou ese desexo.
No momento de comezar a súa carreira (esperou un ano desde o remate do bacharelato polo complicado da situación política que se vivía), na Universidade de Santiago de Compostela só se ofertaban dous cursos que debían ser completados noutra Universidade se se quería obter o título de licenciado. Este foi o motivo de que se desprazase á Universidade Central de Madrid para cursar a licenciatura de Matemáticas que estreaba esta denominación, en vez de Ciencias Exactas, e que pasaba a ter unha duración de cinco anos en vez de catro.
Ao chegar a Madrid, en 1945, María instalouse na Residencia de Señoritas da rúa Fortuny e permaneceu nela durante toda a carreira. Ademais de dedicarse ás matemáticas, seguiu cultivando e formándose noutras afeccións como a música, os idiomas ou os deportes.
Tras unha brillante carreira, desexaba poder continuar os seus estudos e atopar un traballo acorde coa súa formación. Coñecedores da súa valía e das mínimas posibilidades que tiña na España da época, algúns dos seus profesores, entre os que se atopaba Julio Rey Pastor, animárona a pedir as bolsas que existían naquel momento para irse ao estranxeiro.
Pouco despois, no 1953 obtivo unha bolsa Fulbright. Converteuse así na primeira española en obter unha destas bolsas para realizar estudos de doutoramento en Matemáticas nos EE.UU. Tras un curso intensivo de inglés, foi enviada á Universidade de Yale, onde se doutorou en 1957 co traballo titulado On the Group of Similitudes and Its Projective Group, dirixido polo prestixioso matemático Nathan Jacobson. Ese mesmo ano regresou a Madrid e alí permaneceu tres anos como bolseira no Instituto Matemático Jorge Juan do CSIC. Lamentablemente, a súa tese americana non lle foi recoñecida en España e tivo que realizar outra aquí dirixida polo profesor Germán Ancochea.
De novo, ante as poucas perspectivas laborais en España e coa proposta de colaborar co matemático Israel Halperin, aceptou unha bolsa postdoutoral para acudir á Queen University (Kingston, Ontario). Logo da súa situación como bolseira, conseguiu un posto de profesora na Universidade de Toronto, sendo naquel momento a única muller no cadro de profesorado. Alí dirixiu a súa primeira tese de doutoramento, a de Robert Moody, hoxe prestixioso alxebrista. Con esa tese aparece a famosa teoría das “álxebras de Kac-Moody”, que deu lugar a un campo moi extenso de traballo.
Permaneceu seis anos en Canadá e, posteriormente, en 1967, trasladouse á Indiana University (Bloomintong, EE. UU.). Na web actual de dita universidade, podemos atopar diferentes referencias a María Wonenburger; en particular, pódese ver o seu contrato inicial nesa Universidade. Alí permaneceu ata 1983, na categoría de Full Professor, a máis alta como docente.
En 1983, por razóns familiares (a enfermidade da súa nai), María Wonenburger abandonou a súa carreira docente e investigadora e regresou a España. Ao longo da súa curta vida académica, publicou máis dunha vintena de artigos en revistas de impacto internacional e dirixiu oito teses de doutoramento. Ademais, realizou a revisión duns 55 traballos, distintos libros e artigos relacionados coa súa investigación, como se pode ver na web MathSciNet.
A importancia das súas contribucións demóstrase coa repercusión que han ter non só en Matemáticas, senón tamén na Física de Partículas ou na Informática. Na actualidade os seus artigos seguen a ser amplamente citados xa que os seus resultados e os dos seus discípulos son usados en gran cantidade e variedade de traballos.
Hai que destacar tamén a riqueza dos seus contactos persoais e as súas colaboracións con matemáticos da talla de Jean Dieudonné, H.S.M. Coxeter, Max Zorn ou Gian-Carlo Rota, ademais dos xa citados Julio Rey Pastor ou Nathan Jacobson. Entre os seus discípulos atópanse matemáticos de gran prestixio internacional como o xa mencionado Robert Moody ou Stephen Berman, que falan dela con veneración recordando como lles facía sentirse seguros para sacar o mellor deles mesmos; e comentan a capacidade que tiña para dirixilos, para orientalos na elección dos temas de traballo con mais posibilidades, para que gozasen coa investigación.
María Wonenburger posuía esa intuición matemática que só teñen algunhas persoas para descubrir novos temas de estudo, e contaba cunha formación sólida e un coñecemento amplo no seu campo que lle permitiu crear novas teorías. Realizou unha labor investigadora no sentido máis moderno da palabra, acudindo a congresos, relacionándose cos matemáticos punteiros do momento, movéndose entre universidades, dando a coñecer os seus resultados a outros investigadores e, o máis difícil, investigando non para si mesma senón para crear unha escola de renome internacional.
María Wonenburger mantivo un discreto retiro na cidade da Coruña, case sempre rodeada dun reducido grupo de matemáticos/as moi conscientes da súa valía. Aínda que tardíos, nos últimos anos da súa vida recibiu unha serie de homenaxes e recoñecementos por parte das sociedades de matemáticas e doutras institucións: socia de honra da Asociación Galega de Profesorado de Ensinanza das Matemáticas (AGAPEMA) e da Real Sociedad Matemática Española (RSME), o nomeamento como doutora honoris causa pola Universidade da Coruña en 2010 ou a creación por parte da Xunta de Galicia do premio María Wonenburger, que anualmente se concede a algunha científica galega con méritos destacados na súa investigación. O concello no que naceu, Oleiros, inaugurou un fermoso parque co seu nome no 2011. A cidade da Coruña conta cun monolito na súa honra no Paseo das Ciencias do parque de Santa Margarita e recentemente inaugurou unha rúa que leva o seu nome.
Síntese do seu labor científico
A Teoría de Grupos Clásicos e as Álxebras de Clifford son, entre outros, temas centrais na investigación de María Wonenburger. Os traballos de J. Dieudonné, publicados a principios dos anos 50 do século pasado, foron estudados por María Wonenburger achegando relevantes melloras nas caracterizacións dalgúns grupos.
O concepto de Álxebra de Clifford unifica conceptos xeométricos de diferentes estruturas alxébricas que foron xurdindo en aplicacións da Física: Os números complexos, as matrices, os cuaterniones, tensores, espinores, etc., son conceptos que apareceron ao longo dos anos e que permiten describir os espazos tridimensional e catrodimensional, o espín do electrón, ou a relatividade especial entre outros. Esta idea resultou tamén de gran utilidade en aplicacións á Xeometría (destacando para a Xeometría de Riemann), Física e a Informática (en particular para o recoñecemento de imaxes); está intimamente relacionada coa teoría das formas cuadráticas e as transformacións ortogonais. Na actualidade, o estudo destas álxebras é un tema vixente en Física-Matemática para describir as propiedades dos obxectos no espazo tempo e do propio espazo.
Doutra banda, da man de María Wonenburger, dirixindo ao seu primeiro alumno de doutoramento, Robert Moody, iniciouse o que co tempo coñecemos baixo o nome de Teoría de Kac-Moody. Actualmente, as álxebras introducidas por Moody na súa tese doutoral (e por V. G. Kac independentemente) son unha clase de álxebras, na súa maioría de dimensión infinita, asociadas a certos xeradores e relacións. As mais sinxelas son chamadas afíns, que tamén foron introducidas na súa tese.
En 1994, durante o XX Colloquium on Gruop Theoretical Methods in Physics celebrado en Xapón, Victor Kac e Robert Moody recibiron o premio Wigner Medal polos seus traballos iniciados en 1967 sobre a teoría dunha nova clase de álxebras de dimensión infinita que actualmente son coñecidas baixo o nome de ambos (álxebras de Kac-Moody) e que teñen un gran impacto en Física, en particular en Física de partículas, Teoría de campos e en Teoría de cordas.
Os traballos publicados por María Wonenburger son amplamente citados. Por exemplo, o último ano da súa estancia en Toronto, 1966, publicouse o seu artigo “Transformations which are products of two involutions” no Journal of Mathematics and Mechanics, que foi referenciado en máis de 30 traballos de relevancia internacional.
Bibliografía:
Fontes impresas:
O listado da súa produción científica pode consultarse no extra correspondente.
Bibliografía secundaria:
Notices of the American Mathematical Society, December 1995; p. 1543.
PUJALES, X.E. (2007): María Wonenburger ou a paixón pola investigación matemática, Gamma, 7: 107-109.
SAMPAYO YÁÑEZ, M. (2003): María Josefa Wonenburger Planells, Gran Enciclopedia Galega, XLIV: 140.
SOUTO SALORIO, Mª J. & TARRIO TOBAR, A. D. (2006): María Josefa Wonenburger Planells. Mujer y matemática, La Gaceta de la RSME , vol. 9.2: 339-364.
Como citar: Tarrío Tobar, Ana Dorotea : Souto Salorio, María José : María Josefa Wonenburger. Publicado o 5/6/2018 no Álbum de Galicia (Consello da Cultura Galega) https://consellodacultura.gal/album-de-galicia/detalle.php?persoa=4247. Recuperado o 18/04/2024
DOCUMENTACIÓN DE
Referencias bibliográficas das recensións elaboradas por María Josefa Wonenburger Planells
Documento elaborado pola Comisión de Igualdade do CCG (2010)
Fonte: elaboración propia
«Aplicación dun pequeno teorema»
Artigo de María Josefa Wonenburger publicado en: Gamma, IES Sofía Casanova de Ferrol, nº 4 (setembro 2004), p. 35.
Fonte: Revista Gamma
«General theory of Lie algebras by Yutze Chow, Gordon and Breach»
Artigo de María Josefa Wonenburger publicado en: Bulletin (New Series) of the American Mathematical Society, v. 1, nº 6 (1979), p. 978-985.
Fonte: projecteuclid.org/
«A generalization of Z-groups»
Artigo de María Josefa Wonenburger publicado en: Journal of Algebra, v. 38, nº 2 (1976), p. 1091–1099.
Fonte: biblioteca de María Josefa Wonenburger
BERMAN, S.; MOODY, R.; WONENBURGER, M.ª J.: «Cartan Matrices with Null Roots and Finite Cartan Matrices»
Artigo publicado en Indiana University Mathematics Journal, v. 21, n.º 12 (1972), p. 1091-1099.
Fonte: iumj.indiana.edu
«Automorphisms of Cayley algebras»
Artigo de María Josefa Wonenburger publicado en: Journal of Algebra, v. 12, nº 3 (1969), p. 441–452.
Fonte: biblioteca de María Josefa Wonenburger
«An introduction to nonassociative algebras by R.D. Schafer»
Artigo de María Josefa Wonenburger publicado en: Bulletin of the American Mathematical Society, v. 75, nº 4 (1969), p. 712-714.
Fonte: projecteuclid.org/
«Noncommutatuve rings by I. N. Herstein»
Artigo de María Josefa Wonenburger publicado en: Bulletin of the American Mathematical Society, v. 75, nº 15 (1969), p. 714-717.
Fonte: projecteuclid.org/
« Transformations which are products of two involutions»
Artigo de María Josefa Wonenburger publicado en: Journal of Mathematics and Mechanics, v. 16, nº 4 (1966), p. 327–338.
Fonte: iumj.indiana.edu/
«Simultaneous diagonalization of simetric bilinear forms»
Artigo de María Josefa Wonenburger publicado en: Journal of Mathematics and Mechanics, v.15, nº 4 (1966) 617–622.
Fonte: iumj.indiana.edu/
« The automorphisms of Un+ (k, f) and PUn+ (k, f)»
Artigo de María Josefa Wonenburger publicado en: Revista Matemática Hispanoamericana, v. 4, nº 24 (1964), p. 52–65.
Fonte: biblioteca CFMAC-CSIC
«A decomposition of orthogonal transformations»
Artigo de María Josefa Wonenburger publicado en: Canadian Mathematical Bulletin, v. 7, nº 3 (1964), p. 379-383.
Fonte: /math.ca/cmb/
«The automorphisms of the group of rotations and its projective group corresponding to quadratic forms of any index»
Artigo de María Josefa Wonenburger publicado en: Canadian Journal of Mathematics, nº 15 (1963), p. 302–303.
Fonte: math.ca/cjm/
«Matrix ℵ-rings»
Artigo de María Josefa Wonenburger publicado en: Proceedings of the American Mathematical Society, nº 142 (1963), p. 211–215.
Fonte: ams.org/journals/
«The automorphisms of PS4+ (Q)»
Artigo de María Josefa Wonenburger publicado en: Revista Matemática Hispanoamericana, v. 4, nº 22 (1962), p. 185–195.
Fonte: biblioteca CFMAC-CSIC
«The automorphisms of the group of similitudes and some related groups»
Artigo de María Josefa Wonenburger publicado en: American Journal of Mathematics, nº 84 (1962), p. 600–614.
Fonte: biblioteca de María Josefa Wonenburger
«The automorphisms of PO8+ (Q) and PS8+ (Q)»
Artigo de María Josefa Wonenburger publicado en: American Journal of Mathematics, nº 84 (1962), p. 635–641.
Fonte: biblioteca de María Josefa Wonenburger
«The Clifford algebra and the group of similitudes»
Artigo de María Josefa Wonenburger publicado en: Canadian Journal of Mathematics, nº 14 (1962), p. 45–59.
Fonte: math.ca/cjm/
«Study of certain similitudes»
Artigo de María Josefa Wonenburger: Canadian Journal of Mathematics, nº 14 (1962), p. 60–68.
Fonte: math.ca/cjm/
WONENBURGER, M.ª J., GRÄTZER, G.: «Some examples of complemented modular lattices»,
Canadian Mathematical Bulletin, v. 5, n.º 2, (1962), p. 111-121.
Fonte: math.ca/cmb
HALPERIN, I.; WONENBURGER, M.ª J.: «On the additivity of lattice completeness»
Artigo publicado en Pacific Journal of Mathematics, v.12, n.º 4 (1962), p. 1289-1299.
Fonte: projecteuclid.org
«Anillos de división»
Artigo de María Josefa Wonenburger publicado en: Gaceta matemática, nº 13 (1961), p. 3–8.
Fonte: biblioteca CFMAC-CSIC
«The spin representation of the unitary group»
Artigo de María Josefa Wonenburger publicado en: Memoria Matemática, Instituto «Jorge Juan» de matemáticas, nº 24 (1961).
Fonte: biblioteca de María Josefa Wonenburger
«El grupo simpléctico»
Artigo de María Josefa Wonenburger publicado en: Gaceta matemática, Instituto "Jorge Juan" de Matemáticas & Real Sociedad Matemática Española, nº 3-4 (1960), p. 85–88.
Fonte: biblioteca CFMAC-CSIC
«Study of a semi-involutive similitude»
Artigo de María Josefa Wonenburger publicado en: Revista Matemática Hispanoamericana, nº 420 (1960), p. 34–45.
Fonte: biblioteca CFMAC-CSIC
«Irreducible representations of the projective group of unitarian similitudes»
Artigo de María Josefa Wonenburger publicado en: Revista Matemática Hispanoamericana, v. 4, nº 20 (1960), p. 147–176.
Fonte: Biblioteca CFMAC-CSIC
«The spin representation of the unitary group (I)»
Artigo de María Josefa Wonenburger publicado en: Revista Matemática Hispanoamericana, nº 4 (1960), p. 79–128
Fonte: biblioteca CFMAC-CSIC
«The spin representation of the unitary group (II)»
Artigo de María Josefa Wonenburger publicado en: Revista Matemática Hispanoamericana, nº 20, (1960), p. 238–250.
Fonte: biblioteca CFMAC-CSIC
DOCUMENTACIÓN SOBRE
RÄMÖ, Johanna: «Strongly Real Elements of Orthogonal Groups in Even Characteristic»
Artigo publicado en: Sibirskiĭ Matematicheskiĭ Zhurnal, v. 51, n.º 2 (March-April, 2010), p. 241-248. Toma como referencia o teorema proposto por María J. Wonengurger en 1966 no seu artigo «Transformations which are products of two involutions».
Fonte: maths.qmul.ac.uk
Créditos da Cartografía de Josefa Wonenburger Planells
COORDINACIÓN
Comisión de Igualdade do Consello da Cultura Galega
DOCUMENTACIÓN
Ana Dorotea Tarrío Tobar
Xosé Enrique Pujales Martínez
María José Souto Salorio
Eliseo Fernández Arias
Mariam Mariño Costales
TEXTOS
Ana Dorotea Tarrío Tobar
Mariam Mariño Costales
DESEÑO
Miguel Alonso Fachado
REVISIÓN LINGÜÍSTICA
Begoña Tajes Marcote
Silverio Cerradelo Gómez
REVISIÓN BIBLIOGRÁFICA
Anxos Sumai
TRATAMENTO DIXITAL DE IMAXES
Teresa Navarro Quinteiro
BORRAJO, G.: «María Wonenburger Planells. Insigne galega en terras de América»
Artigo publicado en: Eduga. Revista Galega do Ensino, n.º 57 (2009), p. 8-15.
Fonte: dialnet.unirioja.es
SOUTO SALORIO, M.ª J., TARRÍO TOBAR, A. D.: «Unha científica pioneira: María Josefa Wonenburger Planells»
reNOVA GALIza. Caderno de Pensamento Cívico, n.º 3 (xullo de 2008), p. 29-33.
Fonte: exemplar da Biblioteca do CCG
«A Universidade de Vigo descobre mulleres matemáticas descoñecidas»
Artigo publicado en A Nosa Terra (15-5-2008)
Fonte: anosaterra.org
BUGALLAL, Isabel: «María Wonenburger Planells: tengo una mente abstracta, no soy nada práctica»
Entrevista publicada en La Opinión (14-5-2008)
Fonte: laopinioncoruna.es/
MOLEZÓN, Fernándo: «Disfruto haciendo Sudokus como la que mas»
Entrevista a María Josefa Wonenburger publicada no xornal La Voz de Galicia (9-3-2008).
Fonte: La Voz de Galicia
PUJALES, X. E.: «María Wonenburger ou a paixón pola investigación matemática»
Artigo publicado en Gamma, n.º 7 (setembro de 2007), p. 107-109.
Fonte: dialnet.unirioja.es
«O María Wonenburger premiará o traballo tecnolóxico e científico das mulleres»
Artigo publicado en xornal.com (13-7-2007)
Fonte: xornal.com
ROUCO, Laura: «La cara amable de las matemáticas»
Artigo publicado en La Opinión (11-3-2007)
Fonte: La Opinión
«Premio a la matemática»
Artigo publicado en La Voz de Galicia (8-3-2007)
Fonte: La Voz de Galicia
«Mujeres de ciencias y de letras»
Artigo publicado en La Voz de Galicia (7-3-2007)
Fonte: La Voz de Galicia
«Reseña biográfica de María Josefa Wonenburger»
Publicada no Boletín de la Real Sociedad Matemática Española, n.º 79 (febreiro de 2007), p. 1.
Fonte: rsme.es
VILLOT, José María: «María Wonenbuger en el reino de Einstein»
Artigo publicado en El Ideal gallego (14-1-2007).
Fonte: El Ideal Gallego
CASAL, I. : «María Josefa Wonenburger P.»
Biografía publicada en Investigadoras galegas, Grupo Correo Gallego, 2007, p. 106-107.
Fonte: exemplar da Biblioteca do CCG
ÁLVAREZ, Elisa: «Un homenaje a la Einstein gallega»
Artigo publicado en, La Voz de Galicia (16-12-2006)
Fonte: La Voz de Galicia
KUMAR SINGH, Anupam: «Reality Properties of Conjugacy Classes in Algebraic Groups»
Este powerpoint toma como referencia o teorema proposto por María J. Wonengurger en 1966 no seu artigo «Transformations which are products of two involutions».
Fonte: math.tifr.res.in
«María Wonenburger ou a paixón polas matemáticas»
Artigo publicado en Hipatia, ano 1, n.º 2 (maio de 2006), p. 1 e 4.
Fonte: Hipatia
SOUTO SALORIO, M.ª J., TARRÍO TOBAR, A. D.: «María Josefa Wonenburger Planells: mujer y matemática»
Artigo publicado na Gaceta de la Real Sociedad Matematica Española, v. 9, n.º 2 (2006), p. 339-364.
Fonte: gaceta.rsme.es
TARRÍO TOBAR, A. D.: Discurso no recoñecemento-homenaxe da Unidade Muller e Ciencia á matemática coruñesa María Josefa Wonenburger Planells
Mecanoscrito inédito
Fonte: arquivo de Ana Dorotea Tarrío Tobar.
VINROOT C., Ryan: «A note on orthogonal similitude groups»
Artigo publicado en Linear and Multilinear Algebra, v. 54, n.º 6 (2006), p. 391-396. Toma como referencia o teorema proposto por María J. Wonenburger en 1966 no seu artigo «Transformations which are products of two involutions».
Fonte: math.wm.edu
«Maruja Wonenburguer una mente prodigiosa»
Artigo publicado en Marineda. El Pais estudiantes, (2005-2006)
Fonte: estudiantes.elpais.com
VINROOT C., Ryan: «Twisted Frobenius-Schur indicators of finite symplectic groups»
Artigo publicado en Journal of Algebra, v. 293, n.º 1 (2005), p. 279-311. Toma como referencia o teorema proposto por María J. Wonenburger en 1966 no seu artigo «Transformations which are products of two involutions».
Fonte: math.wm.edu
KUMAR SINGH, Anupam: «Reality properties of conjugancy Classes in G2»
Artigo publicado en Isreal Journal of Mathematics, n.º 145 (2005), p. 157-192. Toma como referencia os teoremas propostos por María J. Wonenburger nos seus artigos «Transformations which are products of two involutions» de 1966 e «Automorphisms of Cayley Algebras» de 1969.
Fonte: arxiv.org
SAMPAYO YÁÑEZ, M.: «María Josefa Wonenburger Planells»
Entrada biográfica na Enciclopedia Galega, 2003, XLIV, p. 140.
Fonte: exemplar da Biblioteca do CCG
Yik-Hoi Au-Yeung: «A necessary and sufficient condition for simultaneous diagonalization of two hermitian matrices and its application»
Artigo publicado no Glasgow Mathematical Journal, n.º 11 (1970), p. 81-83. Toma como referencia o teorema proposto por María Josefa Wonenburger en 1969 en «Simultaneous diagonalization of symmetric bilinear forms»
Fonte: http://journals.cambridge.org/action/
Ligazóns de interese
O fío de Penélope. O novelo de María Josefa Wonenburger Planells
Elena Vázquez Cendón fai unha achega a María Josefa Wonenburger Planells e os seus vínculos e relacións no portal do CCG
[última consulta: 13/01/2023]
Nota sobre o falecemento de María Josefa Wonenburger Planells no web da RSME
Elaborada por Nerea Díez López
[última consulta: 16/12/2022]
María Josefa Wonenburger Planells é unha das protagonistas do seminario Matemáticas x matemáticas
[última consulta: 16/12/2022]
María Josefa Wonenburg Planells en mulleresconciencia.com
[última consulta: 02/01/2022]
María Josefa Wonenburger na wikipedia
[última consulta: 02/01/2022]
María Josefa Wonenburger na UDC
[última consulta: 02/12/2022]
María Josefa Wonenburger, una olvidada matemática con dos tesis… que nadie reconoció en España
[última consulta: 01/12/2022]
Premio María Josefa Wonenburger. Unidade Muller e Ciencia de Galicia
[última consulta: 16/12/2022]
Xenealoxía matemática de María Josefa Wonenburger
[última consulta: 16/12/2022]
María Josefa Wonenburger, la gallega que amaba las matemáticas
Conto de Olalla Cernuda ilustrado por Laura Sánchez-Ostiz
[última consulta: 16/12/2022]
Créditos da biobibliografia do “cartografías” do Álbum de mulleres
COORDINACIÓN
Comisión de Igualdade do Consello da Cultura Galega
DOCUMENTACIÓN
Ana Dorotea Tarrío Tobar
Xosé Enrique Pujales Martínez
María José Souto Salorio
Eliseo Fernández Arias
Mariam Mariño Costales
TEXTOS
Ana Dorotea Tarrío Tobar
Mariam Mariño Costales
DESEÑO
Miguel Alonso Fachado
REVISIÓN LINGÜÍSTICA
Begoña Tajes Marcote
Silverio Cerradelo Gómez
REVISIÓN BIBLIOGRÁFICA
Anxos Sumai
TRATAMENTO DIXITAL DE IMAXES
Teresa Navarro Quinteiro
Agradecementos da biobibliografia do “cartografías” do Álbum de mulleres
PERSOASFernando Bellas
Covadonga Blanco García
Manuela Candal Garaboa
Concepción Díaz-Fierros Tabernero
Elena Fraboschi
Ana María Fraga Vila
Enrique Macías Virgós
Xosé Enrique Pujales Martínez
María José Souto Salorio
INSTITUCIÓNS
Biblioteca CFMAC-CSIC
Canadian Mathematical Society
Facultade de Matemáticas da Universidade de Santiago de Compostela
Radio Galega
Real Sociedad Matemática Española (RSME)
Universidade da Coruña
COLECTIVOS
Asociación Galega do Profesorado de Educación Matemática (AGAPEMA)
Foro Cívico Galego de Barcelona
XORNAIS E REVISTAS
Boletín de la Real Sociedad Matemática Española
Bulletin of the American Mathematical Society
Canadian Journal of Mathematics
Canadian Mathematical Bulletin
Eduga. Revista Galega do Ensino
Gaceta de la Real Sociedad Matemática Española
Gaceta Matemática
Hipatia. Boletín de Divulgación Matemática
El Ideal Gallego
Indiana University Mathematics Journal
Journal of Mathematics and Mechanics
Marineda. El país de los estudiantes
Memoria Matemática
La Opinión de A Coruña
Pacific Journal of Mathematics
El País
reNOVA GALIza. Caderno de Pensamento Cívico
Revista Gamma
Revista Matemática Hispanoameriacana
La Voz de Galicia
Videos
O fío de Penélope (2/11) [2020]: E. Vázquez Cendón explora o universo de M. J. Wonenburger no CCG [2010]
Elena Vázquez Cendón, decana de Matemáticas da Universidade de Santiago de Compostela, coordinadora da Sección de Ciencia, Tecnoloxía, Natureza e Sociedade e membro do Plenario do Consello da Cultura Galega, tira do fío de María Josefa Wonenburger Planells, a segunda muller homenaxeada no ciclo coa xornada MJWP na creación de coñecemento, realizada en 2010. A súa navegación lévanos por referencias vitais que marcaron a obra da científica coruñesa como foron o gusto pola arte, o ensino das novas xeracións, a importancia da docencia ou o inxente labor das mulleres pioneiras na ciencia. Todo isto baixo o paraugas do sorriso de María que alumea o seu legado para as novas xeracións.
María Wonenburger: la felicidad de las matemáticas, por Pilar del Castillo (21-05-2011)
[última consulta: 16/12/2022]
Montaxe fotográfica sobre a entrevista que lle realizaron no programa da Radio Galega Efervescencia a María Josefa Wonenburger (16-9-2007)
CCG
Inauguración do monolito dedicado a María Josefa Wonenburger (02/06/2011)
[última consulta: 16/12/2022]
Audios
Presentación de María Josefa Wonenburger Planells na creación de coñecemento
Entrevista a María Josefa Wonenburger
Referencias bibliográficas
- PUJALES, X.E.: “María Wonenburger ou a paixón pola investigación matemática”, Gamma, n.º 7 (2007), p. 107-109.
- SAMPAYO YÁÑEZ, M.: “María Josefa Wonenburger Planells”, Gran Enciclopedia Galega, 2003, XLIV, p. 140.
- SOUTO SALORIO, M.J.; TARRÍO TOBAR, A.D.: “María Josefa Wonenburger Planells. Mujer y Matemática”, Gaceta de la RSME, v. 9, n.º 2 (2006), p. 339-364.
Libros do ccg sobre María Josefa Wonenburger
Álbum da ciencia.
2018 | Francisco Díaz-Fierros Viqueira, Coordinación. Xosé Antón Fraga, Coordinación. Alfonso Mato, Coordinación.
: 30 nomes e as súas achegas